
Vanderbilt’s Vito Quaranta, M.D., right, Alissa Weaver, M.D., Ph.D., and Peter Cummings, Ph.D., worked with Alexander Anderson, Ph.D., of the University of Dundee, Scotland, (on video monitor) to develop a math model to help predict tumor behavior.
Photo by Susan Urmy
Math model predicts tumor behavior
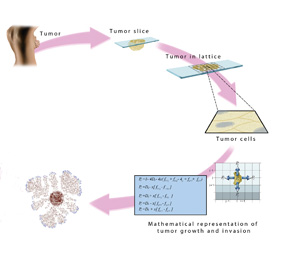
Mathematical modeling of cancer behavior may be useful in the future for predicting tumor growth and guiding treatment options. The modeling can be thought of as a slice of tumor “growing” on a mathematical lattice. Mathematical equations drive a computer simulation of tumor growth, allowing physicians to determine if the cancer will become invasive and metastatic.
Graphic by Dominic Doyle
Vito Quaranta, M.D., clicks on a small black dot on his computer screen. The dot — which represents about a thousand cancer cells — begins to “grow,” morphing into a mass with finger-like projections that looks like an invasive tumor.
Quaranta, professor of Cancer Biology, envisions a future when computer simulations like this will be used to predict a tumor's clinical progression and help formulate treatment plans.
It's not so different from forecasting the weather, he said.
“Today we can know pretty well that for the next few days we're going to expect good weather or that there's a storm on the way,” Quaranta said. “That's the kind of predictive power we want to generate with our model for cancer invasion.”
Quaranta and colleagues at Vanderbilt University and the University of Dundee in Scotland describe a mathematical model for cancer invasion in the current issue of the journal Cell. The model — a series of mathematical equations that drive computer simulations of tumor growth — suggests that the microenvironment around tumor cells determines the tumor's ultimate cellular makeup and invasive potential.
The investigators have focused on the events of invasion and metastasis (movement of a tumor to distant sites), Quaranta said, because these events mark “the critical transition of a tumor that in the end will be lethal for the patient.” A tumor that does not penetrate the surrounding tissue can often be surgically removed with curative success.
“When a patient comes in with a tumor, we'd like to understand for that particular tumor, what are the chances that metastasis is going to occur?” Quaranta said. “Does that patient need to be treated very aggressively, or not so aggressively?”
Today, a tumor's size and shape are evaluated, but they can be poor indicators of invasive potential: a very small tumor can be highly invasive. Even “molecular signatures” — profiles of molecules that suggest how tumor cells will behave — are not entirely predictive, he added.
Quaranta and colleagues opted for a new approach — using the tools of mathematics to tackle the complex problem of cancer behavior.
The scientific team includes core members Alexander Anderson, Ph.D., senior lecturer (associate professor) in the Department of Mathematics at the University of Dundee, Peter Cummings, Ph.D., John R. Hall Professor of Chemical Engineering at Vanderbilt, and Alissa Weaver, M.D., Ph.D., assistant professor of Cancer Biology at Vanderbilt, working with a highly interactive and interdisciplinary group of cancer biologists, bioengineers, imaging scientists, computational biologists and mathematicians.
Armed with funding through the National Cancer Institute's Integrative Cancer Biology Program, the group began two years ago to develop an interdisciplinary approach to studying cancer invasion, based on mathematical modeling. The initial result, published as an entirely theoretical paper in Cell, represents a sea change in “how biology is being done,” Quaranta said.
“We have mathematics driving experimentation,” he said. The team will tailor its biological experiments to test and validate the model. If the experimental data don't fit the predictions from the model, either the experiments or the model need to be corrected, he said.
“You go back and forth, and every time you get a new result, you correct the model, and you're a little bit closer to reality,” Quaranta said. “This is a paradigm that is new to experimental biology.”
“What is happening in biology is similar to trends seen in recent decades in the physical sciences,” Cummings said. “Computational models like this, in which complex behavior emerges from computer simulations grounded in understanding phenomena at a smaller scale, have been a staple of chemistry, physics, and related engineering disciplines for a long time.”
Quaranta and Cummings expect to see this new way of thinking sweep through biology.
“Particularly in cancer biology, we know so much about tumors, but we can do so little: Why is that?” Quaranta said. “I think the reason is that we need additional tools, and those are the tools of mathematics.”
The team's model is “an initial effort,” Quaranta said. It is sophisticated enough to begin capturing tumor behavior, without being so complicated that computing power and time for simulations become limiting. The current model simulates about four months of tumor growth in about eight hours, he said.
“The beauty of our model is that it really represents the cancer cells very well,” Quaranta said. “Sandy (Anderson) was able to capture the random behavior of cells.”
In the model, cells can — each time they divide — randomly choose from a set of 100 different “phenotypes” — behaviors that result from distinct genetic characteristics. For example, a cell might choose characteristics that allow it to divide more quickly or to detach from its neighbors. The investigators set the environmental conditions: these include the oxygen and nutrient concentrations and the landscape of connective tissue that surrounds the cells.
The investigators were surprised to find that the microenvironment around the tumor determines both the tumor's shape and its composition.
“What we get is a picture of cells that are evolving and growing within a microenvironment,” Quaranta said. “The nice thing about computer simulations is you can create 'what if' scenarios: What if we make the oxygen very high, what if we turn oxygen off in the middle of tumor growth? What if we change the landscape of connective tissue?
“By doing this we discovered new things that we didn't know before. And that is the hallmark of a good mathematical model: It's not just a repository of data that is put together; it actually tells you which variables are the important ones and gives outcomes that you wouldn't have otherwise predicted.”
The current model predicts that in mild environmental conditions — imagine a lush rainforest, Quaranta said — many cell types co-exist and the tumor shape is round with smooth edges, characteristic of a non-invasive tumor. Under harsh environmental conditions — imagine a desert — the most aggressive cell types dominate and the tumor shape has fingering, invasive projections.
By changing a single condition — oxygen concentration — the investigators can modulate the tumor's degree of invasiveness, Quaranta said.
The findings suggest that current chemotherapy approaches which create a harsh microenvironment in the tumor may leave behind the most aggressive and invasive tumor cells.
“In the immediate term we may be diminishing tumor burden, but the long-term effect is to have a much nastier tumor than there was to begin with,” Quaranta said. There is anecdotal evidence, he added, to support the idea that changes to the microenvironment result in a tumor with more or less invasive potential. Such manipulations of the microenvironment could offer new directions for cancer treatment, he said.
Next up for the group are in vitro and in vivo experiments designed to test, validate and refine the mathematical model.













